Category: Graphing and Transformation

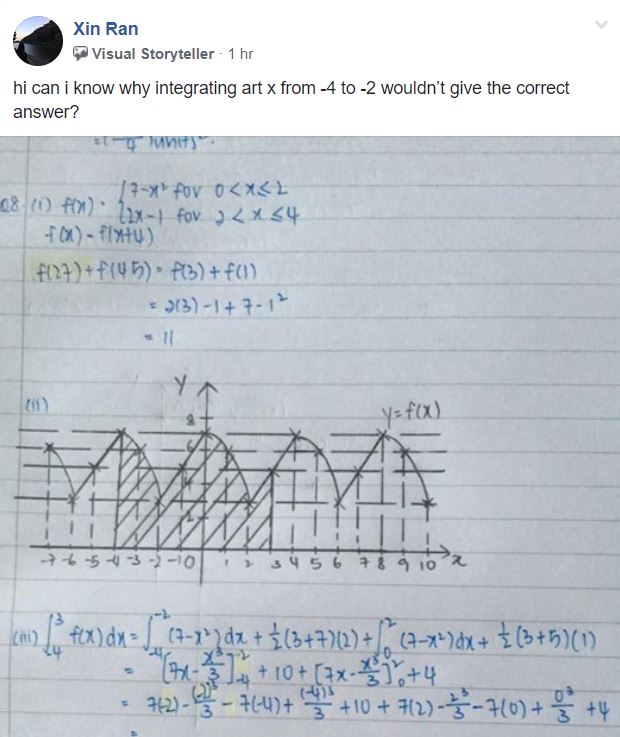
Common error in area of periodic functions

common error

common error1

How to sketch both cartesian and parametric graphs on the same diagram using GC

Example 

DHS 2018 J1 Aug test

Suppose we want to sketch the curve C and the line y=-2x+2 on the same graph

DHS 1

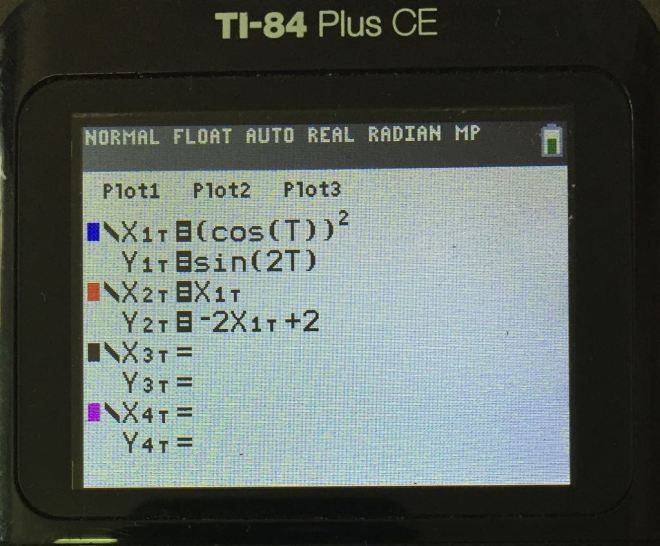
Note how the line y-2x+2 is entered.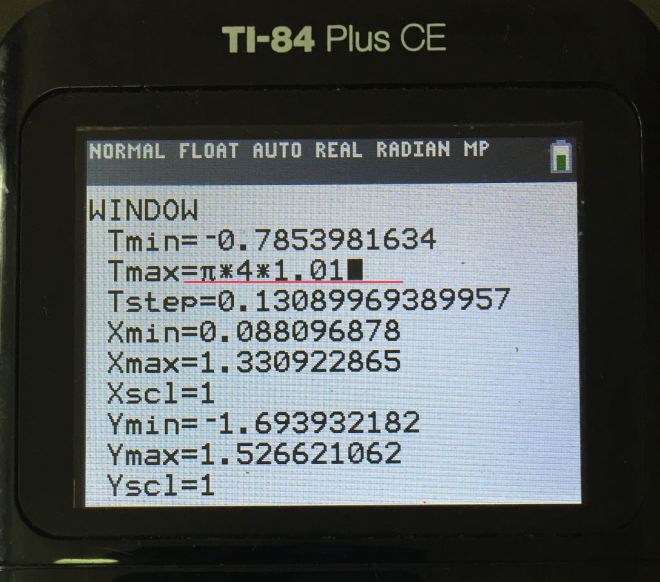DHS 2

Adjust the Tmax to 1%  more so the graph displays correctly.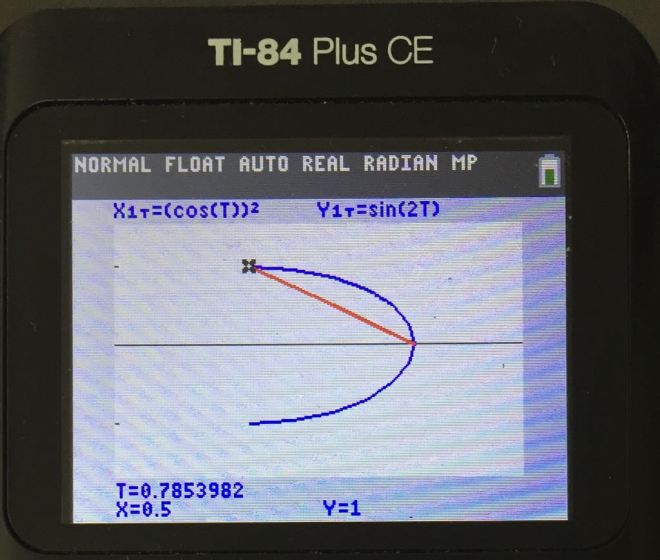DHS 3

Finding sequence of transformation

Usually the sequence of transformation can be found by the replacement method. However, it can be tough to find the replacement for complicated functions. For such cases, we can use the general linear transformation c f(bx+a)+d to find the sequence.

cf(bx+a)+d = Translate by a units in the negative X direction, then scale by a factor of 1/b parallel to the X-axis, then scale by a factor of c parallel to the Y-axis, then translate by d units in the positive Y direction.

Example

NYJC 2016 prelim

Solution

NYJC 2016. alterativeJPG

Sketching Periodic functions with GC

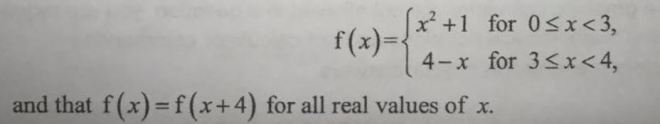
Periodic function 0 sketch from -3 to 8

Suppose we want to sketch the graph from -3 to 8.

  1. Enter by pressing “Math, Piecewise”.

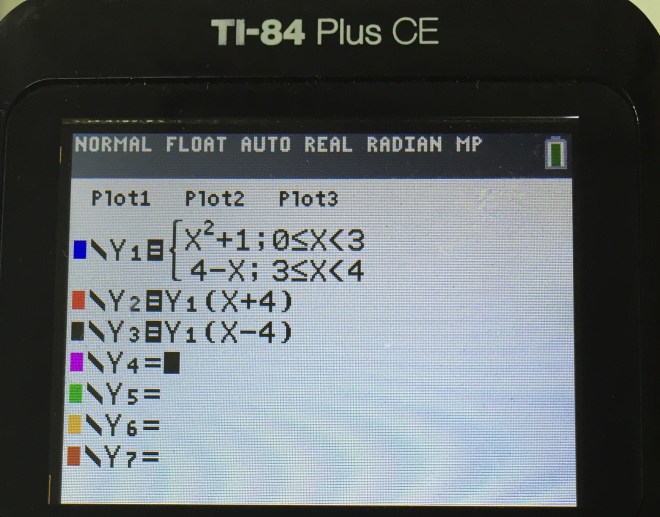
periodic function 1

2. Adjust the window setting to the required domain.

Periodic function 2

3. Trace the end point at -3 since it is not 1 complete cycle.

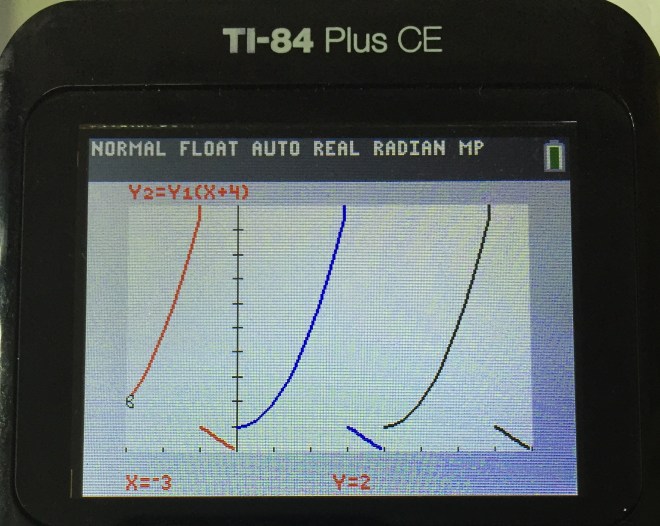
Periodic function 3

How to check Sequence of Transformation?

sequence of transformation check

Advanced graph transformation

Advanced graph transformation can be done in stages, using the replacement method. Each time, we replace x or y.

advanced transformation 1

advanced transformation 2

Challenging graphing technique question 1

This question was posted by a student at Singapore JC maths.

question

Solution for Part ii

1

Graph transformation of oblique asymptote

Many students have difficulty with the graph transformation of oblique asymptote. Consider the oblique asymptote y = x-1 (red line)

oblique

i) y= 1/ f(x)

f(x) approaches infinity as x approaches infinity. 1 divided by infinity is 0.

Hence oblique asymptote y=x-1 becomes horizontal asymptote y= 0

For y= 1/ f(x), any oblique asymptote y=ax+b in f(x) will become horizontal asymptote y= 0 

ii) y= f ‘ (x)

The gradient of y= x-1 is 1. Hence oblique asymptote y=x-1 becomes horizontal asymptote y= 1

For y= f ‘ (x), any oblique asymptote y=ax+b in f(x) will become horizontal asymptote y= a

iii) y= f(2x+1)

Let original asymptote be f(x) = x-1

Therefore, f(2x+1) = (2x+1)-1 = 2x

Hence oblique asymptote y = x-1 is transformed to y=2x.

This method can be applied to any oblique asymptote.

Reverse graph transformation

This question was posted by a student.

” What is the series of transformation from f(3-x/2) to f(x)?”

Here are 3 different methods to solve it.

Method 1

Let f(3-x/2) = g(x)

Let u=3-x/2

x= -2u+6

f(u)=g(-2u+6)

f(x)=g(-2x+6)

Therefore, the sequence of transformation is

Translate 6 units in the negative X direction.

Scale by a factor of 1/2 parallel to the X-axis.

Reflect about the Y-axis

Method 2a

Apply f(-2x) to f(3-0.5x).

f(-2x) = f[3-0.5(-2x)] = f(x+3)

ie. Scale parallel to the X axis by a factor of 0.5. Then reflect about the Y axis

Apply f(x-3) to f(x+3) to get f(x)

ie. Translate 3 units in the positive X direction

Method 2b

Apply f(x+6) to f(3-0.5x) to get f(-0.5x)

ie. Translate 6 units in the negative X direction.

Apply f(-2x) to f(-0.5x) = f(x)

ie. Scale parallel to the X axis by a factor of 0.5. Then reflect about the Y axis.

Method 3

f(3-x/2) is transforming f(x) by

Ａ：Translate 3 units in the negative X direction

B: Scale by a factor of 2 parallel to the X axis

C: Reflect about Y axis.

So to get back f(x), we reverse the transformation:

C’: Reflect about Y axis

B’: Scale by a factor of 1/2 parallel to the X-axis.

A’: Translate 3 units in the positive X direction

Comments

Method 1 and 2 are the forward approach. Method 3 is the reverse approach.

Method 1 is the preferred approach as it is easier and faster.