

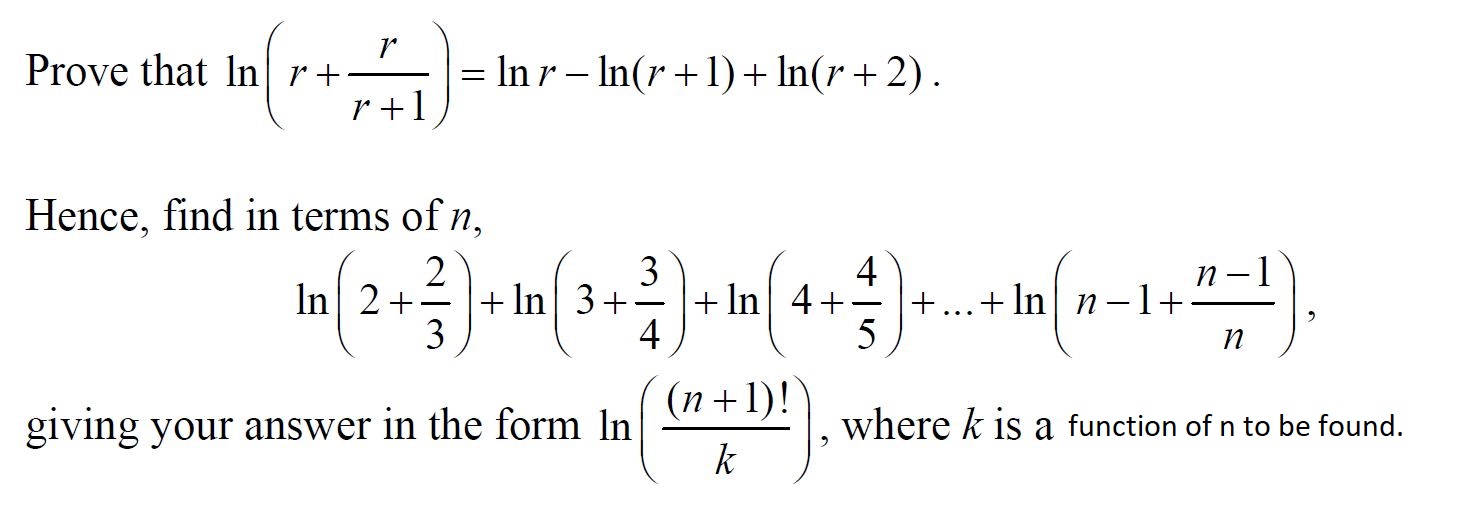
Solution for the Hence portion:
These are the more challenging alevel questions mentioned in the examiner’s report:
2022 P1: 3b, 4c, 5, 9b i, 11d, 12c
2022 P2: 2b, 2c, 3c, 5c, 6, 9b, 11c, 11e
2021 P1: 4bii, 6c, 11
2021 P2: 2, 3b ii, 5c, 7b, 8c, 10e, 11
2020 P1: 4ii, 5, 9i, 10, 11
2020 P3: 3ii, 4iii b, 8ii, 9iv
2019 P1: 8b, 8c, 9, 10 iv,
2019 P2: 1 iii, 2i, 6i, 6ii, 7v, 8 iii, 9i, 10i
2018 P1: 6,9 iii, 10, 11
2018 P2: 6,7,9v
2017 P1: 5ii, 6, 7ii, 8, 9c, 11 iii
2017 P2: 1 ii, 2 ii, 3a, 4b, 7i, 9v, 9 vi
2016 P1: 3, 4, 6 iii, 7, 8 iii, 10 bii, 11 b
2016 P2: 2a ii, , 2b, 4bii, 7 iv, 9a
2015 P1: 3, 5 iii, 7iii, 11 ii explain why is maximum, 11 iii
2015 P2: 1 ii, 2ii, 3b, 4b iii (some students interpret wrongly), 9 ii, 9 iii, 10 iv, 11 iv
2014 P1: 2, 3, 4ii, 6 (a) (ii), 6 (b) (ii), 7 iii, 7 iv, 8 iii, 9 iii, 10 ii, 10 iv, 11 iii, 11 iv
2014 P2: 1 ii, 3 ii, 4 b ii, 6 ii, 6 iii, 10 ii
2013 P1: 2, 5, 6i, 6 iii, 8 i, 9 ii, 9 iii, 10 i, 10 iii, 11 ii, 11 iv
2013 P2: 1 ii, 2, 3 iii, 4iii, 6, 7 i, 8 iii, 9 i, 10 i, 11
2012 P1: 4, 5, 6 iii, 7 iii, 8 iii, 9 iii, 10, 11
2012 P2: 1 b, 3 ii, 3 v, 4, 6ii, 7 iii to v, 8 iii, 8 vii
2011 P1: 1, 3 iii, 4 i, 5 iii, 7 ii b, 8 c, 9 ii, 10 ii
2011 P2: 2 ii, 3 ii, 3 iii, 8 i, 9ii b, 10 iii, 11 ii
2010 P1: 1 ii, 6 iii, 6 iv, 7, 9, 10 i, 11 ii, 11 iii
2010 P2: 1 ii, 3 iii, 4v, 7iv, 7v, 8ii, 8iii, 10 iv
2009 P1: 1 ii, 2, 4, 10 iii, 11 iv
2009 P2: 1 i, 1 iii, 2 iii, 2 iv, 3, 4, 6 ii, 6 iii, 6 iv, 7, 8iii, 8iv, 9 iv, 11 i, 11 ii, 11 v
2008 P1: 1, 5 ii, 6a, 9 ii, 10 ii a, 10 ii b,
2008 P2: 1 iv, 2, 7, 8iii, 8 iv, 10 , 11 last part
2007 P1: 1, 2 i, 5 (hence part), 7i, 10 iii, 11
2007 P2: 2 iii, 2 iv, 3 iii, 4 ii b, 7 last part, 8, 9 (i) (b), 9 (ii) (c), 11
The owner of a restaurant counts the number of banquets received by the restaurant at the end of each week. The probability that the restaurant receives at least two banquets in a randomly chosen week is 0.3. A week is considered busy if the restaurant receives at least two wedding banquets in the week.
Calculate the probability that in a period of 6 consecutive weeks, the 6th week is the second busy week, given that there is at most one busy week in the first four weeks.
Ans: 0.166
Solution
Calculating number of ways of dividing people or distinct objects into groups of the same size often pose difficulty to students.
Hopefully these examples will help students understand the concept.
Basic Example
How many ways can 10 children be divided into two groups of 5?
When dividing people or distinct objects into groups, if p groups are indistinguishable, we need to divide by p! to avoid double counting.
Challenging example 1
At a particular reception, 9 guests are to stand at 3 identical round tables. How many ways can this be done if there are at least two people at each table?
Challenging example 2 (SAJC 2011/MYCT/2/6)
This challenging question on normal distribution was posted in Edusnap by a student.
There were two mistakes made:
1) Interpreting the distribution of 2 large hampers and n small hampers as 2L + nS.
2) Calculation of variance
Here is the correct solution:
Smallest possible value of n = 9
————————-
When the question mentions n items, the distribution is X1+X2+…Xn. When the question asks for “n times of a randomly chosen..”, then the distribution is nX.
Students also need to be familiar with calculating the expectation and variance of the sum or difference of normal distribution using the formula:
You must be logged in to post a comment.