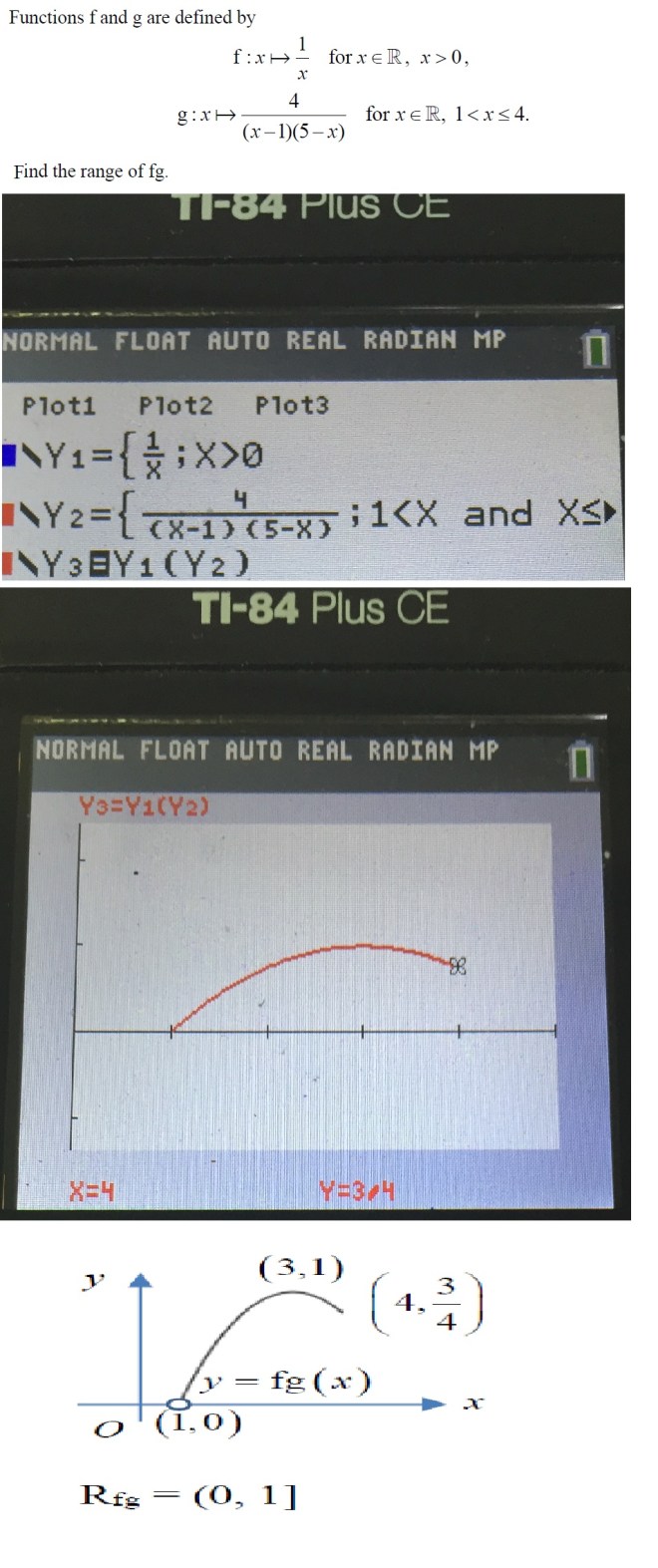
Finding range of composite functions using GC


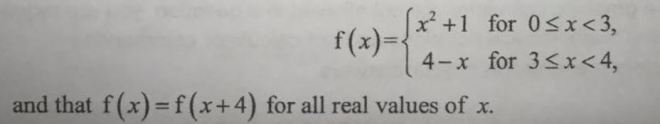
Suppose we want to sketch the graph from -3 to 8.
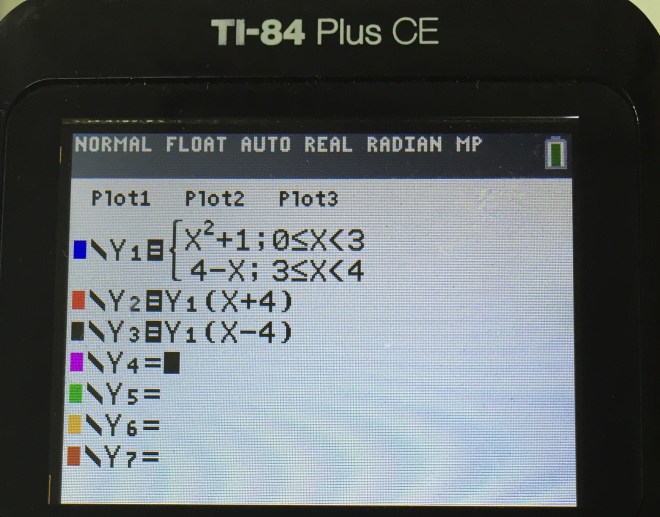
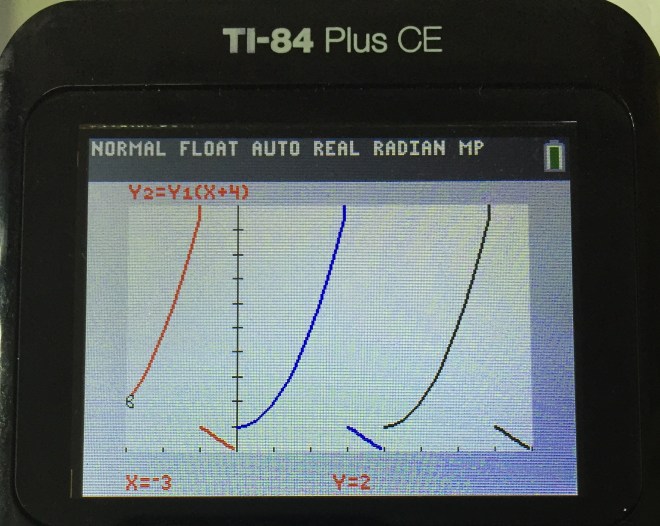
2. Adjust the window setting to the required domain.

3. Trace the end point at -3 since it is not 1 complete cycle.
H2 math syllabus 9740 did not state that periodic functions are included in the syllabus. However, questions on periodic functions have appeared in A level 2009 and 2013.
So it is good to learn periodic, even and odd functions.
Periodic functions
A periodic function has a graph with a basic pattern that repeats at regular intervals.
For example, sin x is periodic and its period is 2 pi.
sin(x) = sin(x+ 2pi)
For a periodic function with period a
f(x) = f(x+a) = f(x+2a) = ..
Simiarly
f(x) = f(x-a) = f(x-2a) = …
i.e. f(x) = f(x+ka) where k is an integer
Even functions
A function is said to be even if f(x) = f(-x) for all values of x. The graphs of all even functions are symmetrical about the vertical axis.
Odd functions
A function is odd if f(x) = -f(-x) for all values of x. The graphs of all odd functions are symmetrical about the origin. One section of the graph can be rotated about the origin through 180 degrees to give the other section.
You must be logged in to post a comment.