In the transformation of graphs, knowing the order of transformation is important. Knowing whether to scale or translate first is crucial to getting the correct transformation.
Let’s look at this example to illustrate the difference:
Example 1
Original point on y=f(x) is x=8
For f(2x+4), we do translation first, then scaling. ie. Move left by 4 units, then scale parallel to the X axis by a factor of 1/2. Hence, the original point becomes x= (8-4)/2 = 2
If we want to do scaling first, we need to factorise into f 2(x+2). So scale parallel to the X axis by a factor of 1/2, then move left by 2 units. Hence, the original point becomes x= (8/2)-2 = 2
Example 2
Describe the transformation of 3f(2x-4) + 5.
Translate 4 units in the positive X direction
Scale by a factor of 1/2 parallel to the X axis
Scale by a factor of 3 parallel to the Y axis
Translate 5 units in the positive Y direction
In summary,
cf(bx+a)+d = Translate by a units in the negative X direction, then scale by a factor of 1/b parallel to the X-axis, then scale by a factor of c parallel to the Y-axis, then translate by d units in the positive Y direction.
c[f a(x+b)]+d = Scale by a factor of 1/a parallel to the X-axis, then translate by b units in the negative X direction, then scale by a factor of c parallel to the Y axis, then translate by d units in the positive Y direction.
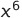
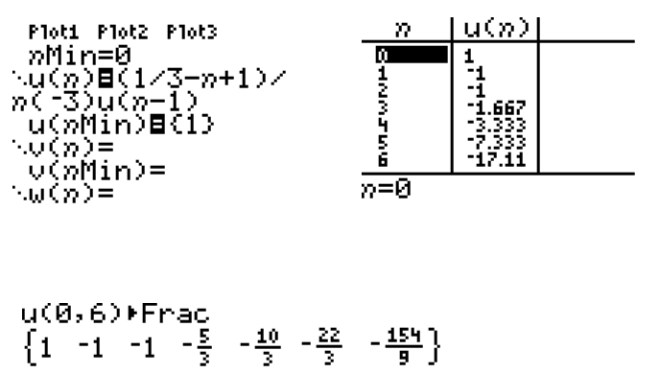
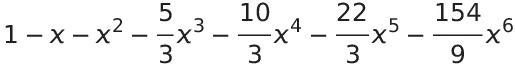
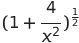





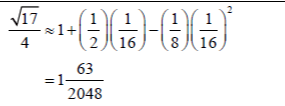
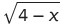
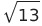
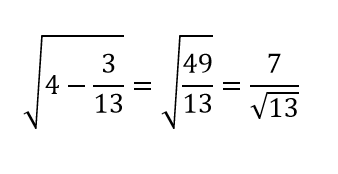


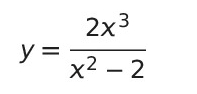
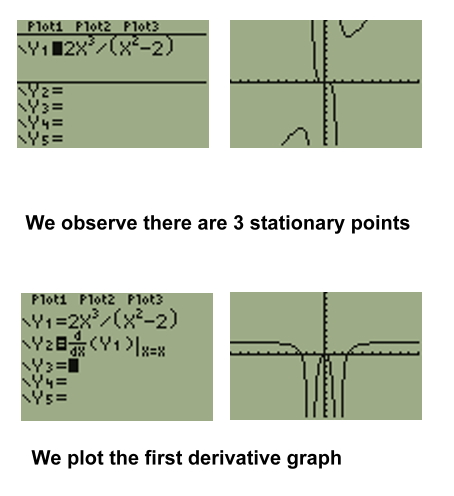


You must be logged in to post a comment.