The following example illustrates how we can use GC in Differential equations, and avoid the need to do integration to solve differential equation.

Solution for part ii

The following example illustrates how we can use GC in Differential equations, and avoid the need to do integration to solve differential equation.

Solution for part ii

GC can be very helpful in solving certain problems in Complex Numbers.
Example 1
Use the GC to find the real value of k such that 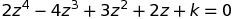 has a complex root 1-i.
has a complex root 1-i.
Solution
Since 1-i is a root,
Using TI 84 Plus (OS 2.55) to evaluate the complex numbers, we have
2+k = 0
k=-2
Example 2
Solution
Since the equation is quadratic, we can use the quadratic formula.
Using the GC to evaulate the above,
z = 1+2i or -7i
There are a total of 20 amusement rides in a theme park. A child insists on trying at least 5 of the amusement rides. Calculate the number of ways in which this can be done.
Answer: 1042380
Solution
Method 1
20 choose 5 + 20 choose 6 +… 20 choose 20
Using TI 84 OS (2.55)
sum (seq(20 nCr X, X, 5, 20, 1)
= 1042380
Method 2
2^20- (20 choose 0+ 20 choose 1+20 choose 2+20 choose 3+ 20 choose 4)
=1042380
In Maclaurin’s series expansion, where up to f”(0) need to be evaluated, can be done quickly using the GC.
Example
Using TI 84 Plus (OS 2.55)
From G.C,
f(0)= 3/2
f'(0) = -3/4
f”(0)= 5/4
Therefore using Maclaurin’s series expansion,
If powers higher than 2 such as 3 are required, then do differentiation to find the first derivative. Then enter into Y1. Y2 and Y3 will then give the second and third derivative.
Binomial expansion can be done quickly using the GC.
Consider binomial expansion of 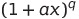 , where a is a real number, and q is a fraction or negative integer.
, where a is a real number, and q is a fraction or negative integer.
The recurrence formula for the coef works out to be
Example 1
Expand 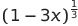 in ascending powers up to and including the term in
in ascending powers up to and including the term in 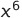
Using TI 84 Plus (OS 2.55)
Therefore, the expansion is
The recurrence formula can also be used to expand in descending powers of x.
Example 2
Expand 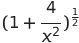 in descending powers of x up to the 7th term.
in descending powers of x up to the 7th term.
Using TI 84 Plus (OS 2.55)
Therefore, the expansion is
All the functions of TI 84 Plus series of calculators are essentially the same and can be used in Alevel.



Suppose we are required to determine the nature of stationary points for the following:
Observation of stationary points:
Left stationary point: First derivative changes from +ve to -ve. Therefore, it is a maximum point
Middle stationary point: No change in sign of deriative. Therefore, it is a point of inflexion.
Right stationary point. First derivative changes from -ve to +ve. Therefore, it is a minimum point
You must be logged in to post a comment.