Complex numbers – JC A Level H2 Math Tuition Singapore

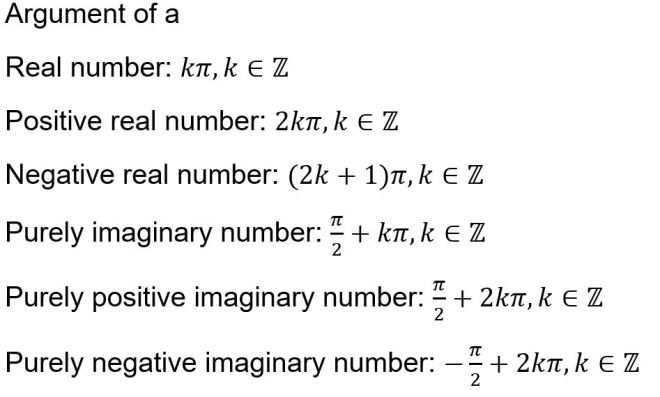
Argument of Real and Purely Imaginary Numbers

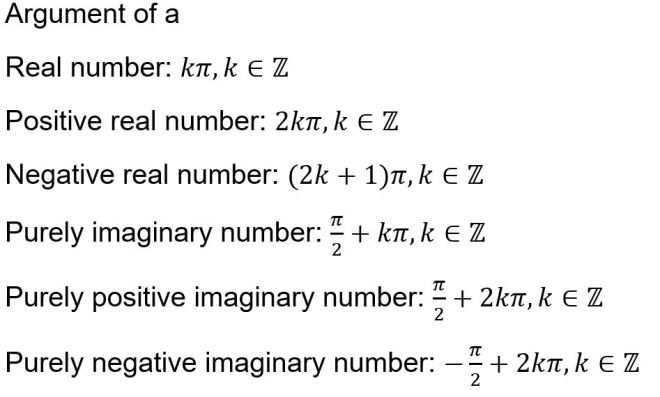
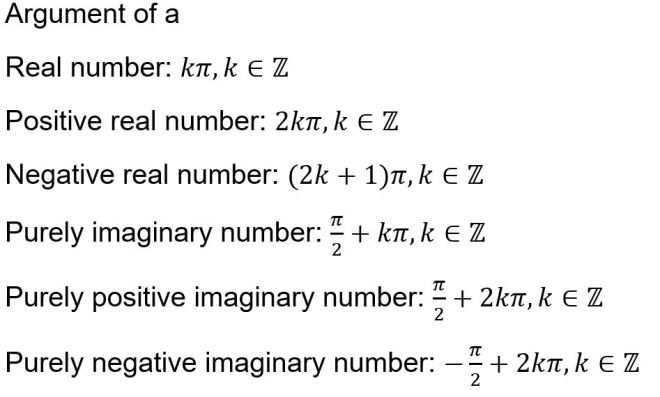
4a argument of real and imaginary

synthetic division in complex numbers

GC can be very helpful in solving certain problems in Complex Numbers.

Example 1

Use the GC to find the real value of k such that 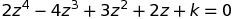has a complex root 1-i.

Solution

Since 1-i is a root,

Using TI 84 Plus (OS 2.55) to evaluate the complex numbers, we have

2+k = 0

k=-2

Example 2

Find the 2 roots of

Solution

Since the equation is quadratic, we can use the quadratic formula.

Using the GC to evaulate the above,

z = 1+2i or -7i

Many students, including JC H2 math students, have difficulty doing long division when it comes to complex problems.

Try this problem to test or sharpen your long division skills.

Question

If is a factor of , prove by long division that

Solution